10292. Моортал
Каубат
Бесси
уже долгое время играет в популярную игру Moortal Cowmbat. Однако недавно разработчики выпустили обновление,
которое вынудило её изменить привычный стиль игры.
В игре
используется m кнопок, обозначенных первыми m строчными
буквами латинского алфавита. Любимая комбинация ходов Бесси – это
строка s длины n,
описывающая последовательность нажатий кнопок. После обновления каждое комбо
должно состоять из последовательности “полос”, где
полоса определяется как непрерывная последовательность нажатий одной и той же
кнопки длиной не менее k. Бесси хочет изменить свою любимую
комбинацию так, чтобы получить новую строку той же длины n, но
состоящую из полос, удовлетворяющих новым правилам.
Известно,
что Бесси требуется aij дней, чтобы научиться нажимать кнопку j вместо
кнопки i в любом конкретном месте комбинации (то есть замена
одной буквы i в строке s на букву j стоит aij дней).
Обратите
внимание, что иногда замена может быть выполнена быстрее через промежуточные
кнопки: например, переход с i на j напрямую
может быть дороже, чем последовательные замены i → k
→ j. Таким образом, может существовать цепочка
преобразований из
i в j, имеющая
меньшую общую стоимость, чем прямая замена.
Помогите
Бесси определить минимальное количество дней, необходимое для создания
комбинации, удовлетворяющей новым требованиям.
Вход. Первая строка содержит три
числа: n (1 ≤ n ≤ 105), m (1 ≤
m ≤ 26) и k (1 ≤ k ≤ n).
Вторая
строка содержит строку s.
Далее
следуют m строк,
каждая из которых содержит m целых чисел – элементы матрицы aij, где aij
– это количество дней, необходимых для замены кнопки i на
кнопку j. Гарантируется, что 0 ≤ aij
≤ 1000 и aii = 0 для всех i.
Выход. Выведите
минимальное количество дней, необходимое Бесси для создания комбинации,
соответствующей новым правилам.
|
Пример
входа |
Пример
выхода |
|
|
5
5 2 abcde 0
1 4 4 4 2
0 4 4 4 6
5 0 3 2 5
5 5 0 4 3
7 0 5 0 |
5 |
|
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Запустим алгоритм Флойда-Уоршелла
на матрице aij, чтобы определить кратчайшее время
замены каждой буквы на любую другую букву.
Составим матрицу стоимостей cst такую что cst[i][j] (1 ≤ i ≤ n) содержит наименьшее
количество дней, за которое можно изменить букву s[i – 1] на
букву j.
Для удобства дальнейших вычислений построим
матрицу ps, содержащую значения частичных сумм матрицы стоимостей cst по столбцам:
ps[i][j] = cst[i][1]
+ cst[i][2] + … + cst[i][j]
Пусть dp[i][j]
содержит
наименьшее количество дней, за которое можно преобразовать первые i букв строки s в строку, удовлетворяющую
новым требованиям Бесси, причем последние k букв в новой
строке будут буквой j.
Запишем уравнения динамики:
·
Пусть первая i – 1 буква строки s уже преобразована в
строку, в которой последними k буквами стоит
буква j. Тогда
мы просто изменяем букву s[i – 1] на j, что
можно сделать за
cst[i][j] дней.
dp[i][j] = dp[i – 1][j] + cst[i][j]
·
Чтобы в новой строке последними k
буквами была
буква j, рассмотрим значения
dp[i – k][0], dp[i – k][1], …, dp[i – k][m – 1]. Выберем среди них наименьшее. То есть
преобразуем первые i – k букв строки s в строку, удовлетворяющую
новым требованиям Бесси (при этом нам не важна буква, которой будет
оканчиваться подстрока длины i – k, нам важно чтобы эту
строку получить за наименьшее количество дней). После чего k
последних букв s[i – k], s[i – k + 1], …, , s[i – 1] исходной строки s меняем
на букву j, на что уйдет
cst[i – k + 1][j] + cst[i – k + 2][j] + … + cst[i][j]
дней.
Указанную сумму можно вычислить за константное время, используя массив
префиксов ps:
cst[i – k + 1][j] + cst[i – k + 2][j] + … + cst[i][j] = ps[i][j] – ps[i – k][j]
Будем поддерживать
дополнительный массив mn, где
mn[i]
= min(dp[i][0], dp[i][1],
…, dp[i][m – 1])
Таким образом, уравнение динамики для этого случая (i
≥ k) будет иметь вид:
dp[i][j] = ps[i][j] – ps[i – k][j] + mn[i – k]
Остается среди двух вариантов для dp[i][j] выбрать наименьшее.
Ответом на задачу будет значение
mn[n]
= min(dp[n][0], dp[n][1], …, dp[n][m – 1])
Нам не важно, на какие именно k букв заканчивается новое слово
Бесси.
Пример
В
данном примере оптимальное решение заключается в следующем: заменить a на
b, затем d на e, а после этого обе e – на c.
Общая стоимость изменений составит 1 + 4 + 0 + 0 = 5 дней, а итоговая строка
будет иметь вид bbccc.
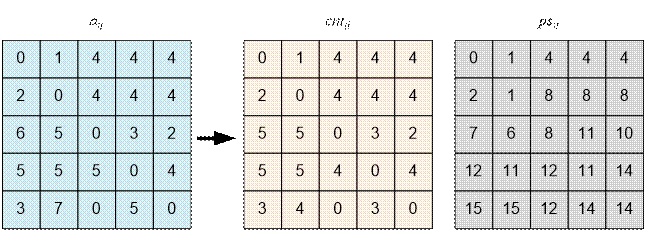
По матрице aij
построим матрицу стоимостей cst. Вычислим также матрицу ps.
Все значения dp[1][j] (0 ≤ j
≤ 4) будут
равны +∞ так как длина полосы не может быть меньше k
= 2. Соответственно mn[1] = +∞.
Рассмотрим процесс вычисления значений dp[2][j] (0 ≤ j ≤ 4).
·
dp[2][0] = (“ab” → “aa”) = cnt[‘a’][‘a’]
+ cnt[‘b’][‘a’] = 0 + 2 = 2;
·
dp[2][1] = (“ab” → “bb”) = cnt[‘a’][‘b’]
+ cnt[‘b’][‘b’] = 1 + 0 = 1;
·
dp[2][2] = (“ab” → “cc”) = cnt[‘a’][‘c’]
+ cnt[‘b’][‘c’] = 4 + 4 = 8;
·
dp[2][3] = (“ab” → “dd”) = cnt[‘a’][‘d’]
+ cnt[‘b’][‘d’] = 4 + 4 = 8;
·
dp[2][4] = (“ab” → “ee”) = cnt[‘a’][‘e’]
+ cnt[‘b’][‘e’] = 4 + 4 = 8;
mn[2]
= min(dp[2][0], dp[2][1], dp[2][2], dp[2][3] , dp[2][4]) = 1
При вычислении значений dp[3][j] (0 ≤ j ≤ 4) уравнение
dp[3][j] = ps[3][j] – ps[1][j] + mn[1]
использовано не будет, поскольку mn[1]
= +∞.
Поэтому для получения полос из первых 3 букв можно лишь
продолжить уже построенные полосы длины 2:
·
dp[3][0] = dp[2][0] + cst[‘c’][‘a’]
= 2 + 5 = 7 (“aaa”);
·
dp[3][1] = dp[2][1] + cst[‘c’][‘b’]
= 1 + 5 = 6 (“bbb”);
·
dp[3][2] = dp[2][2] + cst[‘c’][‘c’]
= 8 + 0 = 8 (“ccc”);
·
dp[3][3] = dp[2][3] + cst[‘c’][‘d’]
= 8 + 3 = 11 (“ddd”);
·
dp[3][4] = dp[2][4] + cst[‘c’][‘e’]
= 8 + 2 = 10 (“eee”);
Значение dp[4][0] можно получить двумя способами:
·
dp[4][0] = dp[3][0] + cst[‘d’][‘a’]
= 7 + 5 = 12 (“aaaa”);
или
·
dp[4][0] = ps[4][0] – ps[2][0] + mn[2] = 12 – 2 + 1 = 11 (“bbaa”)
Второй случай оптимальнее, дописываются две буквы ‘a’
к строке из двух символов. Значение mn[2]
= 1 достигается
на строке “bb”, а значит
оптимальной строкой будет “bbaa”.
Реализация алгоритма
Объявим рабочие массивы:
·
a[i][j] – минимальная стоимость превращения
буквы i в букву j.
·
cst[i][j] – стоимость того, чтобы i-я
буква исходной строки s (индексация начинается с 1) была заменена на
букву j. Формально
cst[i][j] = a[s[i - 1] - 'a'][j]
·
ps – массив частичных сумм по cst, чтобы быстро находить
стоимость изменения подстроки длиной k:
ps[i][j] = cst[1][j] + cst[2][j] + ... + cst[i][j]
·
dp[i][j] – минимальное
количество дней, чтобы преобразовать первые i букв строки s в допустимую строку (по правилам
полос), при этом
последние k букв результата должны быть буквой j.
·
mn[i] – минимум по всем j из dp[i][j]: лучшее решение для первых i символов.
#define MAXN
100005
#define ALPH 26
int a[ALPH][ALPH], cst[MAXN][ALPH], ps[MAXN][ALPH], dp[MAXN][ALPH],
mn[MAXN];
Читаем входные данные.
cin >> n >> m >> k;
cin >> s;
for (i = 0; i < m; i++)
for (j = 0; j < m; j++)
cin >> a[i][j];
Запускаем алгоритм Флойда-Уоршелла на матрице a. По его
завершению a[i][j] содержит наименьшее количество дней, за которое
можно изменить букву i на букву j.
for (x = 0; x < m; x++)
for (i = 0; i < m; i++)
for (j = 0; j < m; j++)
a[i][j]
= min(a[i][j], a[i][x]
+ a[x][j]);
У нас имеется m ≤ 26 букв. Составим
матрицу стоимостей cst
такую
что cst[i][j] (1 ≤ i ≤ n) содержит наименьшее количество дней, за
которое можно изменить букву s[i – 1] на букву j. Индексация
букв в строке s начинается с 0.
Для удобства дальнейших вычислений построим
матрицу ps, содержащую значения частичных сумм матрицы стоимостей cst по столбцам:
ps[i][j] = cst[i][1]
+ cst[i][2] + … + cst[i][j]
for (i = 1; i <= n; i++)
for (j = 0; j < m; j++)
{
cst[i][j] = a[s[i - 1] - 'a'][j];
ps[i][j] = ps[i - 1][j] + cst[i][j];
}
Инициализируем массивы.
memset(dp,
0x3f, sizeof dp);
memset(mn,
0x3f, sizeof mn);
mn[0]
= 0;
Вычисляем значения ячеек массива dp. Букве i соответствует символ s[i – 1]. Нумерация букв в переменной j идет от 0 (которой соответствует
буква ‘a’) до m – 1. Интуитивно на каждом шаге i Бесси
решает:
·
либо продолжать ту же кнопку, что и раньше,
·
либо начать новую полосу длиной как минимум k.
Мы выбираем, что дешевле, и записываем результат в dp[i][j].
Цикл по i начинаем с k, потому что первая допустимая полоса
может закончиться только на позиции k.
for (i = k; i
<= n; i++)
for (j = 0; j < m; j++)
{
Продолжаем текущую полосу. Букву исходной строки s[i – 1] меняем на j. То есть:
·
предыдущие i – 1 букв уже преобразованы и заканчиваются на j;
·
теперь добавляем i-ю букву s[i – 1], тоже делаем её j;
·
стоимость составит dp[i – 1][j] + cst[i][j].
dp[i][j] = min(dp[i][j], dp[i - 1][j] +
cst[i][j]);
Начинаем новую полосу из k букв. Считаем, что на позиции i
заканчивается новая полоса длиной ровно k (или больше), состоящая из
буквы j. Для этого:
·
Берём лучшее преобразование первых (i – k)
букв (всё, что было раньше): mn[i – k].
·
Добавляем стоимость замены последних k букв (от i
– k + 1 до i) на j:
ps[i][j] - ps[i -
k][j]
dp[i][j] = min(dp[i][j], ps[i][j] - ps[i -
k][j] + mn[i - k]);
После вычисления всех dp[i][j] для фиксированного i, сохраняем
лучшее (минимальное) значение среди всех j в mn[i].
mn[i] = min(mn[i], dp[i][j]);
}
Выводим ответ.
cout
<< mn[n] << "\n";